Ich möchte Ihnen heute eine Lösungsstrategie frei nach den Brüdern Grimm vorstellen. Sie funktioniert in vielen Bereichen. Ich kann aber nicht garantieren, dass sie immer funktioniert …
1. Das Vorbild: das „tapfere Schneiderlein“
Können Sie sich noch an das „tapfere Schneiderlein“ erinnern? Es erschlug „sieben auf einen Streich“ (allerdings nur Fliegen) und machte mit diesem Slogan Karriere am Hof des Königs – ein schönes, frühes Beispiel für eine gezielt platzierte Imagewerbung, die sachlich richtig war und mit einem gewissen „spin“ auch die richtigen Abnehmer fand.
Aber der Karriere am Hof standen trotz gelungener Imagearbeit noch Hindernisse entgegen. Wissen Sie noch? Da waren z.B. 2 Riesen zu besiegen sowie ein Einhorn und ein Wildschwein zu fangen …
Mir geht es jetzt um die 2 Riesen. Wissen Sie noch, wie das Schneiderlein vorging?
Die Riesen lagen schlafend im Gras. Der Schneider kletterte mit Steinen bewaffnet auf einen Baum über den Riesen und warf die Steine nach und nach auf den einen und den anderen. Die beiden Riesen erwachten, dachten – dumm, wie sie waren – der jeweils andere habe den eigenen Schlaf gestört, gingen aufeinander los … und brachten sich gegenseitig um.
2. Problemlösung durch Problemverdoppelung
Das tapfere Schneiderlein hat hier eine Lösungsstrategie gewählt, die man verallgemeinern kann. Man könnte es die Strategie der Lösung durch Eskalation oder der Lösung durch Verdoppelung des Problems bezeichnen. Ein Riese wäre unbesiegbar; zwei Riesen – das doppelte Problem – sind besiegbar, wenn man die beiden „Probleme“ irgendwie auf einander beziehen (sozusagen: auf einander „hetzen“) kann.
Das geht oft; z.B. auch in der Mathematik:
2.1. Mathematik: Bruch- und Dezimalzahlen
Vielleicht wissen Sie noch, dass endliche und periodische Dezimalzahlen und Bruchzahlen das Gleiche sind. Man kann jeden Bruch durch Dividieren in eine Dezimalzahl verwandeln:
5/4 = 5 : 4 = 1,25
7/3 = 7 : 3 = 2,33333…
Entweder kommt eine endliche Dezimalzahl heraus oder eine periodische.
Man kann aber auch jede endliche oder periodische Dezimalzahl in einen Bruch verwandeln:
21,03 = 2103/100
0,507 = 507/1000
usw.
Aber geht das auch bei periodischen Dezimalzahlen? Wie ist das z.B. bei 3,070707…?
Naja: eine periodische Dezimalzahl hat unendlich viele Dezimalstellen. Sie ist sozusagen „ein Riese“. Einen Riesen zu besiegen ist schwer. (Es geht in diesem Fall schon: mit „schwerem Geschütz“ wie der Grenzwertberechnung von Folgen).
Nennen wir den Riesen x und erzeugen einen zweiten Riesen, nämlich 100 x:
| x = | 3,070707… | |||
| 100 x = | 307,070707… |
Wir subtrahieren (= „aufeinander hetzen“) den ersten Riesen vom zweiten:
99 x = 304
und damit:
x = 304 / 99
Wenn Sie jetzt dividieren, bekommen Sie 3,070707…
In der Mathematik kommt diese Lösungsstrategie öfter vor. Z.B. auch in der Integralrechnung:
2.2. Mathematik: Integralrechnung
Es geht hier beispielsweise um ein Integral der Form …
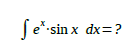Für viele Menschen sind solche Dinge heute noch (oder gerade heute wieder) Ungeheuer … Veritable „Riesen“!
Es gibt die Methode der partiellen Integration; die Umkehrung der Produktregel für das Differenzieren. Sie sagt uns:
Wir fassen im obigen Integral
auf und
.
Dann ist ebenfalls
und
und wir bekommen:
Jesses! Links ein Ungeheuer, rechts ein ähnliches Ungeheuer … aber das macht Hoffnung! Wir ahnen: wir sind gerettet!
Denn nach der gleichen Logik bekommen wir:
und also
Jetzt haben wir das gleiche Ungeheuer links und rechts des Gleichheitszeichens. Das lässt sich zusammenfassen:
bzw:
Problem gelöst. Riese besiegt; nebenbei ist noch der andere Riese ins Netz gegangen.
2.3. Schuladministration: Stundenplanfehler
Ich habe als Schuladministrator Stundenpläne zu machen. Das ist nicht ganz leicht: es gibt pädagogische Notwendigkeiten, es gibt Wünsche von LehrerInnen, es gibt knappe Raumressourcen. Den Stundenplan macht eine Software, die durch Parameter halbwegs geschickt gesteuert werden muss und die dann trotzdem in der Regel noch eine händische Nacharbeitung des maschinellen Stundenplans erforderlich macht.
Einmal ist mir ein gravierender Fehler passiert. Für eine große Klasse waren 2 Gruppen in Englisch vorgesehen. Diese beiden Gruppen waren zu „koppeln“, d.h. die jeweiligen Stunden waren im Stundenplan am gleichen Ort (aber halt in einem anderen Klassenraum) vorzusehen.
Ich hatte die Koppelung übersehen; die Software rechnete im Stundenplan für die ganze Schule für diese Klasse einen Plan mit beiden Englisch-Gruppen an verschiedenen Stellen des Stundenplans aus. Das war natürlich Unsinn, denn immer dann, wenn die eine Englisch-Gruppe Unterricht gehabt hätte, hätten die anderen „frei“ gehabt. Das ist nicht sinnvoll (oder wird nicht als sinnvoll erachtet). Also war der Stundenplan neu zu machen. Das war insofern ein riesiges Problem, als am Stundenplan einer Klasse die Lehrerstundenpläne dieser KlassenlehrerInnen, über diese aber auch die Stundenpläne anderer Klassen und also die der LehrerInnen anderer Klassen hingen. Das hätte bedeutet, für die gesamte Schule wäre der bereits veröffentlichte Stundenplan neu zu machen gewesen. Eine einzige Katastrophe; ein riesiges Problem.
Es tat sich für diese Klasse aber noch ein anderes gravierendes Problem auf. Sie hatte sehr viele Studierende. Das war in Englisch – wegen der Gruppenteilung – kein Problem. Auch in den anderen Fächern ging es sich halbwegs aus. Nur in Mathe war die Gruppe ebenfalls riesig groß, unverantwortlich groß.
Das war der zweite Riese. „Gottseidank“!
Es war nötig und möglich, eine zweite Mathe-Gruppe zu eröffnen … und die beiden Mathe-Gruppen mit den beiden Englisch-Gruppen im Stundenplan zu „kreuzen“. Wenn die einen Englisch hatten, hatten die anderen Mathe; die Mathe der anderen kam dorthin, wo Englisch der einen war. Beide Gruppen bekamen einen in sich logischen Stundenplan ohne „Löcher“; die Mathematik-Gruppen waren akzeptabel groß; beide Englisch-LehrerInnen konnten ihre Pläne behalten und keine anderen Klassen- oder LehrerInnen-Pläne mussten verändert werden.
Beide Riesen besiegt. Die entstandenen Stundenpläne waren „besser“ als jene, die entstanden wären, wenn die Stunden gekoppelt gewesen wären, denn es entstanden Wahlalternativen für jene Studierenden, die Englisch bzw. Mathematik nicht belegen mussten.
2.4. In Sozialstrukturen
Gesetzt den Fall, Sie haben in einer Gruppe eine Person A, die permanent die Arbeit in der Gruppe stört, ein Übermaß an Aufmerksamkeit und Zuwendung benötigt, den Betrieb aufhält. Aus irgendeinem Grund können Sie A nicht kaltstellen, nicht „hinausschmeißen“; Sie und Ihre Gruppe leiden an A.
Doch dann kommt B. B hat bzw. macht ähnliche Probleme. Die Probleme verdoppeln sich. Sie haben 2 Riesen. Jetzt können Sie aufgeben oder …
Sie könnten versuchen, die beiden Riesen auf einander zu „hetzen“. Das muss nicht unfreundlich sein. A könnte sich um B kümmern, B könnte sich um A kümmern. Im Idealfall werden A und B in ihrer Ähnlichkeit ein ausgezeichnetes Team, das zum Erfolg der Gruppe wesentliche Teilergebnisse beiträgt. Ich kann Ihnen nicht garantieren, dass die Methode immer wirkt, aber ich habe hervorragende Beispiele selbst erlebt.
Im kleinen Format habe ich das z.B. einmal in einer Wettbewerbssituation unter 11-jährigen Schülern erlebt. Es waren Gruppen zu bilden; bald hatten sich Gruppen aus je 3 Buben gefunden. Nur 2 wurden in keine Gruppe aufgenommen; sie waren Außenseiter. Einer wäre ein Problem gewesen, zwei waren keines. Ich habe sie dazu ermuntert, sich als Gruppe zu verstehen und sie haben unter den Bubengruppen am besten abgeschnitten – obwohl sie ein Mann weniger waren.
2.5. Politik: das „Zünglein an der Waage“
Eine bekannte Variante der Problemlösung durch Verdoppelung ist in der Politik das „Zünglein an der Waage“. A und B sind viel größer als C, bringen aber jeweils für sich allein keine Mehrheit zustande. Dann kann C immer regieren. Hat C ein Problem mit A, löst es das durch einen Koalitionswechsel zu B. Und umgekehrt. Die beiden Riesen blockieren sich gegenseitig, der Schneider gewinnt. In Deutschland hat die FDP auf diese Weise lange mit SPD bzw. CDU regiert.
Gäbe es nur einen Riesen, hätte C keine Chance und keine Bedeutung.
2.6. Politik: „divide et impera“
Auch das alte römische Prinzip des „teile und herrsche“ funktioniert nach einer ähnlichen Logik. Wenn du einen „riesigen“ Gegner hast: mach zwei (oder mehr) daraus. Spalte den Feind und sorge dafür, dass die beiden Teile auf einander losgehen.
Die Strategie ist allerdings gefährlich. Wenn die verdoppelten Riesen nicht dumm genug sind, sondern die Strategie durchschauen, hast du plötzlich nicht mehr einen Gegner, sondern deren zwei. Wir landen da beim Zauberlehrling, der den Besen spaltet, der Wasser schleppt. Und dann 2 Besen erzeugt hat, die doppelt so viel Wasser schleppen.
Könnte das eine Strategie gegen den Terrorismus sein? Oder verwendet der Terrorismus das bereits als Strategie gegen die westlichen Demokratien?
Lit.:
Koedukation und Mathematik – ein nicht-repräsentatives Ergebnis … enthält ein Beispiel
Der Pistolendreikampf … und das „Beförderungsproblem“ … auch da ist eine Verdoppelung die Lösung
tertium datur … in dem Artikel geht es um „immer nur 2 von 3“, ein ähnlicher Zusammenhang