… aus dem Rätselforum der Schule …
1. Das Rätsel …
… wird gestellt (9.11.2015):
Wir befinden uns in Paris, ca. 1890. Drei noble Herren, nennen wir sie Alexandre, Bernard und Charles, sind in ein ernstes Zerwürfnis geraten. Es geht – wie sollte es in Paris 1890 anders sein! – um die Gunst einer Dame. Und um die Ehre, na klar. Wie das bei noblen Herren so ist: das Problem kann nur durch ein Duell – nein: einen Dreikampf – gelöst werden. Vereinbart wird ein Pistolendreikampf im Morgengrauen.
Die 3 Herren wissen von einander: A trifft immer, B in 4 von 5 Fällen, C nur in 50%. Der erste Schuss wird ausgelost, dann geht es reihum weiter. Jeder darf schießen, wohin er will. Der Dreikampf endet, wenn nur mehr einer übrig ist. Der bekommt die Dame. (Wenn die mitspielt …)
Welcher der 3 Kavaliere hat die besten Chancen und wie hoch sind die ungefähr? (Oder auch exakt, aber das ist nicht leicht.)
Wie sieht es mit den Chancen der anderen aus?
Kann man etwas für ein normales, „bürgerliches“ Leben im 21. Jahrhundert daraus lernen?
Zusatzfrage: Was halten moderne Damen des 21. Jahrhunderts von solchen noblen Herren?
2. Die Lösung
(17.11., nach einigen Tagen Diskussion, einer richtigen Teil-Lösung von Herrn E. und einer – bis auf ein Missverständnis – richtigen Lösung von Koll. G.)
Liebe Rätselfreunde,
hier nun die offizielle exakte Lösung des Rätsels – so exakt war sie gar nicht geplant.
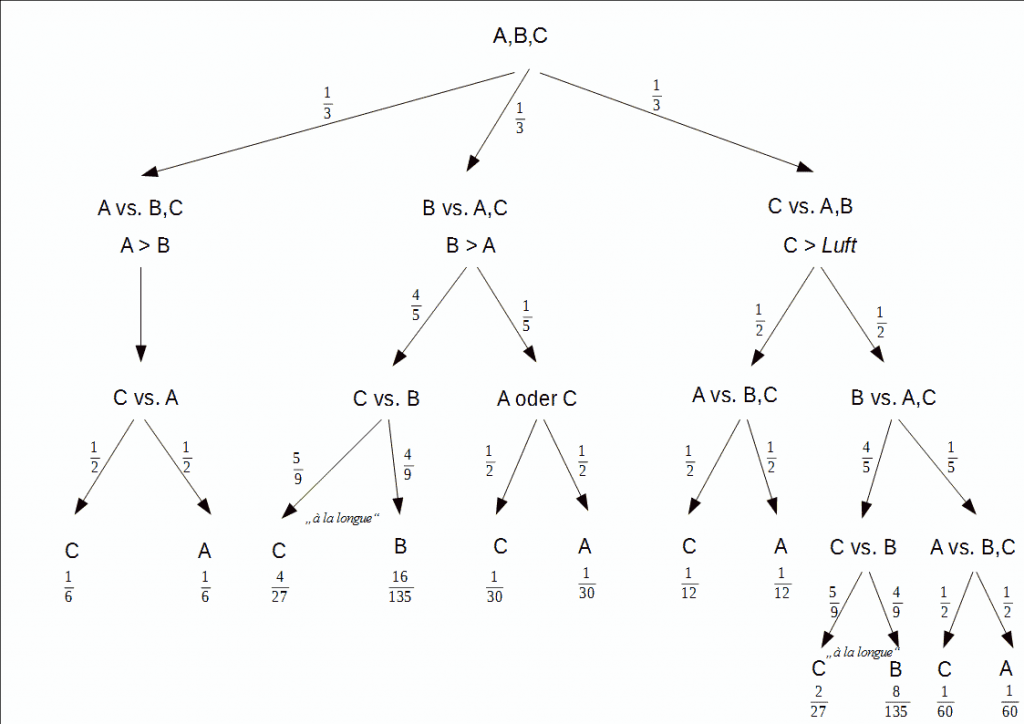
Wenn A als erster Schießender ausgelost wird, wird er vernünftigerweise auf B zielen und ihn eliminieren, denn B wäre ihm im nächsten Gang wesentlich gefährlicher als C. Desgleichen wird B auf A zielen, wenn er ausgelost wird. Und C schießt vernünftigerweise „in die Luft“, wenn er ausgelost wird.
Herr E. hat den Teil mit A gelöst; Koll. G. hat den Entscheidungs- und Ereignisbaum detailliert beschrieben. Der einzige Unterschied zwischen seiner und meiner Lösung ist, dass Koll. G. das Wort reihum so verstanden hat, dass nach A B drankommt, nach B C und nach C jedenfalls A. So war bzw. ist das aber nicht gemeint.
Wenn A gegen C im Finale steht, hat C den ersten Schuss und eine Chance von 50%. Und A hat die anderen 50%. Das hat Herr E. schon gezeigt.
Wenn B gegen C im Finale steht, hat auch C den ersten Schuss. Es entwickelt sich dann ein theoretisch unendlicher Ereignisbaum (die könnten mit einer sehr sehr geringen Wahrscheinlichkeit „heute noch“ schießen), den man zu 5/9 für C und 4/9 für B „kürzen“ kann.
Klar ist: C kann auf jeden Fall ins Finale kommen; er hat dort gegen A die Chance 50% und gegen B sogar 5/9 = 55,55…%. Die Wahrscheinlichkeit, gegen B ins Finale zu kommen, ist etwas geringer als gegen A, weil A den B eher besiegt als B den A.
Insgesamt: C 52,22…%; A 30%; B 17,77…%
Eine halbwegs akzeptable Skizze wäre das:
3. Der Transfer …
… ins 21. Jahrhundert: als „Beförderungsproblem“ (20.11.2015)
Aber zurück ins 21. Jahrhundert. Kann man aus dem Beispiel etwas für unsere Zeit lernen?
Stellen Sie sich vor, es geht nicht um Leben und Tod, sondern um Karriere: Beförderung oder nicht Beförderung. In einer Firma wird eine Stelle frei. 3 MitarbeiterInnen kommen in Frage: A, B und C. A ist super, sozusagen „Mr. 100%“ oder „Miss 100%“; B ist sehr gut, er / sie „gewinnt“ 80% aller bearbeiteten Fälle; C ist sehr bemüht aber noch nicht so erfolgreich, 50%. A, B und C kennen sich gut und wissen um die gegenseitige Stärke. Doch der Personalchef / die Personalchefin (P) weiß das nicht. Er / sie möchte ein Bewerbungsverfahren durchführen…
Wer hat die besten Chancen, den Job zu bekommen?
Was muss A tun bzw. vermeiden, um den Job zu bekommen?
Was muss B tun bzw. vermeiden, um den Job zu bekommen?
Was muss C tun bzw. vermeiden, um den Job zu bekommen?
Was muss P tun bzw. vermeiden, um den / die Beste[n] zu bekommen?
(Ich gebe selbstverständlich zu: die Analogie ist sehr spekulativ. Aber überlegen wir …)
Also als ersten Impuls würd ich vorschlagen:
Ein Personalchef P, der seine BewerberInnen in Duelle schickt, ist ein schlechter Personalchef, eigentlich ein Trottel. Er kriegt mit relativ hoher Wahrscheinlichkeit den schwächsten Bewerber für den Job. Verschachtelte Duelle sind ein mieses Auswahlverfahren.
Was meinen Sie? Und A, B, C?
Hier gab es keine schriftliche Diskussion mehr, ich wurde nur mehr mündlich auf die neue Version angesprochen. Deshalb am 24.11. die Finalisierung:
Liebe Rätselfreunde,
offenbar mag (oder traut sich) niemand über das Beförderungsproblem zu diskutieren. Dann schließ ichs ab:.
Ja, ich glaube durchaus, dass man aus dem Pistolendreikampf-Rätsel den Schluss ziehen kann, dass verschachtelte Duelle kein geeignetes Bewerbungsverfahren sind. Allgemeiner: wenn man in einer Firma ein Klima des „jeder gegen jeden“ schafft, ist das nicht gut: dann kommen oder bleiben nicht „die besten“.
Für die Perspektive von C könnte man lernen: wenn du glaubst, du bist der schwächste Bewerber, versuch dich zunächst zurückzuhalten. Unter Umständen beschädigen sich „die besseren“ selbst und du kommst dann wenigstens in Finale.
Für die Perspektive von A (oder B): wenn du glaubst, du bist echt gut, besser als die anderen: verlass dich nicht drauf. Je nach setting sind deine Chancen gar nicht sooo gut. Lass dich vor allem nicht auf Duelle ein, sondern sorg dafür, dass im Bewerbungsverfahren alle ihre Stärken zeigen können (und müssen).
Möchte noch jemand was ergänzen? Widerspruch?
4. Und die Rolle der Dame? Die Meinung moderner Frauen?
Leider gab es zu dieser Frage nur wenig Diskussion. Mit der Lösung des Problems beschäftigten sich überhaupt nur Männer. Vielleicht gings doch zu sehr um Tod und Schießen. Allerdings gabs in Mails an mich doch 2 Äußerungen von Frauen. Frau P. meinte u.a.:
Es müsste niemand zur Waffe greifen und schießen, wenn sie alle vier (vlleicht sogar KommilitonInnen..) sich einfach die Hand reichen /oder der Dame küssen würden;P) und einen auf den gutn Durst trinkn gehn….
Frau S. wurde durch das Rätsel zu einem längeren, sehr philosophischen Beitrag provoziert. Auf die Rolle der Dame im Rätsel führte sie dabei aus:
Meines Erachtens hat definitiv die Frau die „Arschkarte“ gezogen!
Sei es, weil sie möglicherweise einen Mann bekommt, den sie schlussendlich gar nicht liebt.
Oder sei es, weil sie nicht das gewisse Selbstvertrauen/Selbstbewusstsein hat, den dreien zu sagen:
„Hey Freunde! Ihr braucht euch nicht gegenseitig abschießen. Ich will nämlich garkeinen von euch!“
Offenbar hätten die Damen des 21. Jahrhunderts wirklich die Courage, in den Dreikampf konstruktiv einzugreifen.
erschienen im Rätselforum der Schule, 9.-24.11.2015; hier gekürzt und redigiert