Wahrheiten: Logik vs. Ökonomie
Und was uns ein Handlungsreisender dazu sagt

1. Wahrheit(en) und Ordnung(en)

Nachdenken zwischen Logik, Ökonomie, Politik, Mathematik, Informatik

1.1. Absolute Wahrheit

Wahrheit gibt es als absolute Wahrheit,
als Dogmen,
als Axiome,
als das das Leben bestimmende Wissen.

Als solche führt „Wahrheit“ zur Deduktion; aus „Wahrheit“ leiten sich Grundsätze des menschlichen Lebens ab.

Dieses Verständnis von Wahrheit führt zu Hierarchie als System der menschlichen Verwaltung, denn es benötigt Autoritäten, die die Axiome, die Dogmen verwalten.

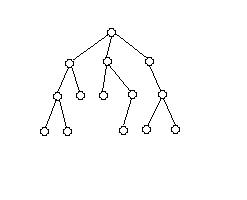
Das Bild dazu ist die Baumstruktur (hier im Aufriss); sie beschreibt sowohl die Verbindungen der „Sätze“ als auch die der menschlichen Beziehungen.

Ein axiomatisches, dogmatisches System wird sehr oft nicht vollständig sein in dem Sinne, dass es für alle Situationen Entscheidungen vorsieht. In diesen Fällen muss das System angepasst bzw. erweitert werden; auch dazu sind Autoritäten, Hierarchien nötig.

Auf alle solchen Systeme ist der Satz von Gödel anwendbar; in etwa: jedes genügend reichhaltige System von Axiomen (insbesondere jedes, das die Zahlentheorie, also das normale Rechnen enthält) enthält zwangsläufig Sätze, die in diesem System nicht beweisbar sind.

Mit anderen Worten: ein deduktives bzw. hierarchisches System kann unmöglich alle Situationen erschöpfend erfassen.

Oder: ein System mit absolutem Anspruch führt sich selbst zwangsläufig logisch ad absurdum.

1.2. Relative Wahrheit

Wahrheit gibt es aber auch als relative Wahrheit;
als Erfahrung,
als empirisches Wissen,
als aus dem Leben abgeleitete Erkenntnis

„Wahrheit“ entsteht hier aus Induktion; aus dieser Perspektive „sind“ Wahrheiten nicht, sondern sie entstehen aus der Praxis, aus Wahrnehmungen. In Bezug auf Wahrnehmungen sind (a priori) alle Menschen gleich. Die entsprechende menschliche Organisationsform ist die Vernetzung, die Anarchie – im Sinne der Abwesenheit von Herrschaft.

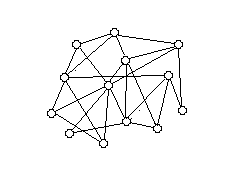
Das Bild dazu ist die Netzstruktur (hier im Grundriss!); sie beschreibt sowohl den Gewinn der Erfahrungen als auch die menschlichen Beziehungen.

Es stellt sich in solchen anarchisch-vernetzten Systemen (oft sehr schnell) die Frage nach der Komplexität der (Zahl der) Beziehungen. n Mitglieder eines Netzwerks können bereits
n · (n – 1) Paare
bzw. n! Anordnungen („Permutationen“) bilden. Mit der Anzahl der Mitglieder der Gruppe steigt die Zahl (und damit die Komplexität) der möglichen Beziehungen enorm, nämlich exponenziell.

Mit dem Problem des Handlungsreisenden (die Frage nach der kürzesten Route zwischen n Kunden, s. Kap. 2) kann man diesen Sachverhalt illustrieren.

Es gibt einige dazu äquivalente Probleme (das „Stundenplanproblem“, das „Kasten-Transport-Problem“, das „Cliquen-Problem“); man nennt sie np-vollständige Probleme.

Es ist derzeit noch unbekannt, ob es für np-vollständige Probleme (die alle prinzipiell endliche Probleme sind!) eine exakte Programmierlösung (also eine optimale Organisationsform) gibt, die bloß polynomialen (i.S.v.: polynomial steigenden) Zeitbedarf erfordert, oder ob diese Probleme mit linearem Wachstum der Population exponenziell wachsenden Zeitbedarf erzwingen … und das hieße, dass sie de facto nicht exakt lösbar wären.

Gibt es keine Lösungen mit polynomial steigendem Zeitbedarf, könnte das bedeuten, dass Induktion / Anarchie mit der Größe der Gruppe, auf die sie sich bezieht, zwangsläufig zum Scheitern verurteilt ist, dass sich menschliche Gruppen ab einer bestimmten Größe also hierarchisch organisieren müssen.

Das hieße, ein induktives, vernetztes, anarchisches System führt sich zwangsläufig ökonomisch ad absurdum.

(Allerdings hat im Jahr 2000 der ukrainische Mathematiker Anatoly D. Plotnikov behauptet, eine polynomiale Lösung vom Grad 6 gefunden zu haben – vgl. „Informatik-Problem P=NP möglicherweise geknackt“)

***

Jedenfalls entsteht zwischen der induktiv-anarchischen und der deduktiv-hierarchischen Perspektive eine Dialektik. Die eine scheitert offenbar ökonomisch, die andere (jedenfalls streng genommen) logisch.

Wäre das „Problem des Handlungsreisenden“ (mit polynomialem Zeitaufwand, also relativ ökonomisch) lösbar, könnte das aber heißen, dass das anarchische Prinzip theoretische Priorität genießt. Dass es also nur darauf ankäme, Netzwerke ordentlich zu organisieren, dass jedenfalls eine (halbwegs) ökonomische Organisation von Netzwerken bzw. anarchischen Strukturen aber prinzipiell möglich ist.

1.3. „Wahrheit“ in (prä-)historischem Zusammenhang

Ich behaupte (nehme an), dass der induktive Wahrheitsbegriff der „ursprüngliche“ ist und dass menschliche Gesellschaften mit zunehmendem Wachstum (von Sippen zu Stämmen, von Stämmen zu Völkern) beginnen, Teile der erkannten Wahrheit(en) axiomatisch / dogmatisch zu verfassen, zunächst mündlich, dann auch schriftlich. Es entstehen dadurch (scheinbar) zwangsläufig Hierarchien (wörtlich übersetzt: „Priesterherrschaften“).

Das würde bedeuten, dass anarchisch-vernetzte Strukturen zwangsläufig nur bis zu einer bestimmten Größe funktionieren können.

Ich halte es aber jedenfalls für möglich, durch moderne Kommunikationsmittel wesentlich größere Gesellschaften als früher anarchisch-vernetzt zu gestalten; das hieße auch, dass Hierarchien eben nicht (oder jedenfalls nicht mehr so schnell) zwangsläufig sind.

1.4. Einige Eigenschaften von Hierarchien und Netzwerken

(Achtung: der hier verwendete Netzwerk-Begriff ist nicht identisch mit dem der Computertechnik. In der Computertechnik gibt es durchaus Netzwerke, die rein hierarchisch sind. Ich nenne Netzwerk, was zusammenhängt und a priori keine „besonderen“ Punkte enthält. Vollständig ist ein Netzwerk, wenn jeder Knoten mit jedem anderen in Beziehung tritt / treten kann.)

Hierarchien

• Jeder zusammenhängende Teil einer Hierarchie ist selbst eine Hierarchie.
• Eine Hierarchie aus n Knoten hat n-1 Beziehungen zu organisieren. (Die Anzahl der zu organisierenden Beziehungen steigt linear mit der Größe der hierarchisch organisierten Gruppe.)
• Bricht eine Hierarchie an einer Stelle, entstehen 2 Hierarchien ohne Zusammenhang.
• Computerbetriebssysteme arbeiten hierarchisch.
• Ein Sportturnier nach dem „K.O.-System“ ist hierarchisch. Nehmen n SpielerInnen teil, benötigt man n-1 Partien.

Netzwerke

• Jede Teilmenge eines vollständigen Netzwerks ist wieder ein vollständiges Netzwerk.
• Ein Netzwerk aus n Knoten hat n . (n-1) Zweierbeziehungen zu organisieren. (Allein die Anzahl der möglichen Zweierbeziehungen in einem Netzwerk steigt quadratisch mit der Größe der vernetzten Gruppe.)
• Ein Netzwerk aus n Knoten hat ca. 2^n = 2ⁿ Teilbeziehungen zu organisieren. (Denn eine Menge aus n Elementen hat 2ⁿ Teilmengen und jeder dieser Mengen entspricht i.W. eine „Beziehung“.) Die Menge der möglichen Teilbeziehungen steigt also nicht quadratisch, sondern exponenziell.
• Bricht in einem Netzwerk eine Verbindung, bleibt der Sachverhalt in aller Regel ein Netzwerk.
• Ein Netzwerk hat a priori keinen ausgezeichneten Punkt. Alle Punkte sind a priori gleichberechtigt. Insofern sind Netzwerke anarchisch.
• Das Internet ist ein Netzwerk, es ist (in wesentlichen Teilen) anarchisch. (Deswegen funktioniert das Internet auch, wenn einzelne Knoten ausfallen.) Ein Netzwerk, eine anarchische Struktur ist nicht „Chaos“. (Chaos nenne ich n Elemente, die keine oder nur zufällige Verbindungen kennen bzw. eingehen.)
• Ein Sportturnier nach dem System „jeder gegen jeden“ baut ein einfaches Netzwerk. Nehmen n SpielerInnen teil, benötigt man (mit Rückspielen) n . (n-1) Spiele.

2. TSP – der „traveling salesman“ durchgeführt

2.1. Das „Problem des Handlungsreisenden“ (traveling salesman problem)

Das Problem: ein Vertreter soll seine Kunden besuchen, jeden einmal. Die Kunden befinden sich an n Orten. Gefragt ist die kürzeste Route.
(Da das Beispiel aus Amerika kommt, ist es populär geworden, an die kürzeste Route zwischen den Hauptstädten der 50 US-Bundes­staaten zu denken, also n = 50.) Sprechen wir von den 9 Landeshauptstädten Österreichs oder den 9 Bezirken Tirols, ist n = 9.

Bsp.: hat der Vertreter die Kunden A, B und C, gibt es folgende 6 Routen:

ABC, ACB, BAC, BCA, CAB, CBA

Sind die Entfernungen AB = 57 km, AC = 64 km und BC = 41 km, so ergibt das als Routenlängen: 98, 105, 121, 105, 121, 98 … die Routen ABC und CBA sind also die kürzesten.

Bsp.: hat der Vertreter die Kunden A, B, C und D, gibt es bereits 24 Routen:

ABCD, ABDC, ACBD, ACDB, ADBC, ADCB, BACD, BADC, BCAD, BCDA, BDAC, BDCA, CABD, CADB, CBAD, CBDA, CDAB, CDBA, DABC, DACB, DBAC, DBCA, DCAB, DCBA

Man versuche z.B. die günstigste Route für die o.a. Entfernungen und zusätzlich AD = 50 km, BD = 28 km, CD = 17 km zu ermitteln.
(Die Streckenlängen bekommt man z.B. als gerundete Längen zwischen den Punkten A = Innsbruck, B = Reutte, C = Landeck und D = Imst.)

Klar ist, dass es jeweils nur endlich viele Routen gibt, dass das Problem also prinzipiell berechenbar ist.

(Um genau zu sein: es gibt n! Routen, wobei paarweise Routen, die genau entgegengesetzt sind, jeweils gleich lang sind. Bei den 9 Landeshauptstädten Österreichs sind das immerhin schon 362.800 verschiedene Routen. Kein Problem für einen halbwegs vernünftigen Computer, aber …)

Es gibt – ob man’s glaubt oder nicht – für dieses Problem derzeit kein allgemeines Verfahren, das in relativ kurzer Zeit eine exakte Lösung erzwingt. Genauer gesagt: es ist mathematisch noch unbekannt, ob dieses Problem mit „polynomialem Zeitverbrauch“ (d.h. de facto: in relativ kurzer Zeit) lösbar ist; derzeit sind nur Verfahren mit dem wesentlich höheren „exponenziellen Zeitverbrauch“ bekannt.)

Beispiel: berechnen wir unter der Voraussetzung, dass für 50 Kunden jede der möglichen Routen 50 Rechenvorgänge erfordert (sukzessive Addition der Teildistanzen) und dass eine gigantische Rechenanlage zur Verfügung steht, die …
1 Billion = 10^12 = 10¹² Rechenschritte pro Sekunde …
ausführt, wieviele Sekunden (Minuten, Stunden, Tage, Jahre) investiert werden müssen, um alle Routenlängen zu berechnen.

50! = 3,04 * 10^64 = 3,04 · 10⁶⁴ Routen

also (mal 50): 1,52 · 10⁶⁶ Rechenschritte

also (dividiert durch 10¹²): 1,52 · 10⁵⁴ Sekunden

also (dividiert durch 60): 2,53 · 10⁵² Minuten

also (dividiert durch 60): 4,22 · 10⁵⁰ Stunden

also (dividiert durch 24): 1,76 · 10⁴⁹ Tage

also (dividiert durch 7): 2,51 · 10⁴⁸ Wochen

oder (dividiert durch 365): 4,82 · 10⁴⁶ Jahre

also (dividiert durch 100): 4,82 · 10⁴⁴ Jahrhunderte =
= 4,82 · 10⁴³ Jahrtausende =
= 4,82 · 10⁴⁰ Jahrmillionen
usw. usf.

(Dem gegenüber wird das Alter des Universums geschätzt auf ca.
15 Milliarden Jahre =
= 1,5 ·  10¹⁰ Jahre =
= 1,5 · 10⁷ Jahrtausende =
= 1,5 · 10⁴ Jahrmillionen)

Mit anderen Worten:

Mit noch so mächtigen Rechenanlagen kann das an sich „billige“ Problem, zwischen 50 Orten die kürzeste Route zu finden, heute nicht in akzeptabler Zeit exakt berechnet werden. Alle unsere Computer zusammen müssten viel länger rechnen als die Welt besteht, um die eindeutig beste Route zu finden.
(!!!)

2.2. Andere derartige Probleme

Es ist mathematisch bewiesen, dass das Problem des Handelsreisenden äquivalent ist mit anderen recht alltäglichen Problemen: dem Kasten-Transport-Problem, dem Stunden­plan­problem u.ä. (das Kasten-Transport-Problem besteht darin, für eine bestimmte Konfiguration von Transportgütern bei einer vorgegebenen Anzahl von Transportmitteln (z.b. LKWs) eine ideale Aufteilung zu finden. Das Stundenplanproblem besteht darin, bei gegebenem Zeitraster für eine Gruppe von Lehrpersonen und eine Liste von Fächern eine Zuordnung zu schaffen, sodass keine Lücke entsteht.) Wenn also für eines dieser Probleme eine Lösung mit polynomialem Zeitbedarf existiert, so ist sie auf die anderen Probleme übertrag­bar.

„Weithin wird angenommen, dass np-vollständige Probleme undurchführbar sind. Obwohl dies noch nicht bewiesen ist, erscheint es […] glaubhaft.“ (Goldschlager / Lister, Informatik 1986). Wie erwähnt: im Gegensatz zur Vermutung von Goldschlager & Lister hat im Jahr 2000 der ukrainische Mathematiker Plotnikov behauptet, eine polynomiale Lösung vom Grad 6 gefunden zu haben. Es ist mir aber nicht gelungen, eine Bestätigung dafür zu finden. Noch immer bzw. verstärkt gehen Publikationen davon aus, dass np-vollständige Probleme für eine exakte Lösung exponenziell (also letztlich über alle Maße) steigenden Zeitbedarf haben.

Plotnikovs Lösung hin oder her: np-vollständige Probleme sind nicht an sich unlösbar; es ist nur so, dass der Aufwand für eine exakte Lösung bei genügend vielen Einheiten schnell über jedes vertretbare Maß steigt. In diesen Fällen ist es sinnvoller, akzeptable Näherungslösungen zu entwickeln.

Dass ein phantasievoller, kreativer, schlauer Mensch (Vertreter, Transportunternehmer, Schuladministrator etc.) das konkrete Problem aufgrund von Erfahrung, Intuition und / oder Genialität trotzdem exakt (und womöglich sogar schnell) löst, ist damit ebenfalls nicht ausgeschlossen. (Man würde jedenfalls als HandlungsreisendeR in Tirol eine Route, die eine Streckenführung Kitzbühel-Reutte-Kufstein-Landeck-Lienz-Imst enthält, von vorherein gar nicht in Erwägung ziehen.)

2.3. Schlussfolgerungen für die Ökonomie

Auch in der Wirtschaftstheorie stehen sich 2 idealtypische Modelle gegenüber: eine strenge Planwirtschaft (ein dogmatisches, hierarchisches System) und eine „freie Marktwirtschaft“, die (zunächst jedenfalls und idealtypisch) anarchisch ist.

Eine ideale (im Sinn von: absolut, kompromisslos durchgeführte) „Planwirtschaft“ würde den Handlungsreisenden Routen vorschreiben.

Eine ideale (im Sinn von uneingeschränkt durchgeführte, kompromisslose) Marktwirtschaft vertraut darauf, dass die Konkurrenz der Handlungsreisenden untereinander dazu führt, dass jeder sich bemüht, immer bessere Routen zu finden, dass sich also die Routenplanungen mittelfristig (quasi) „von selbst“ verbessern. Markt / Konkurrenz führt zu Verbesserungen der Produktion, dem Markt / der Konkurrenz ist also Innovation inhärent … das ist die Grundannahme.

Das traveling salesman problem zeigt: wenn schon ein so verhältnismäßig einfacher Sachverhalt wie das Problem des Handlungsreisenden de facto nicht exakt lösbar ist: wie soll dann eine ganze Volkswirtschaft planbar sein?

Man kann also mit dem traveling salesman problem sozusagen „beweisen“, dass eine absolute Planwirtschaft nicht funktionieren kann.

Es ist damit aber nicht sichergestellt, dass eine Wirtschaft, die lediglich mit der Konkurrenz arbeitet, deswegen schon funktioniert. Wir kennen jedenfalls aus der Wirtschaftstheorie, dass Markt bisweilen dazu führt, dass sich Monopole entwickeln. Dann fällt das Element der Konkurrenz weg; die Marktwirtschaft degeneriert zum quasi-planwirtschaftlichen Ding. Geplant wird dann allerdings nicht mehr durch die gesamte Gesellschaft (bzw. durch ihre demokratisch gewählten Abgeordneten), sondern lediglich innerhalb der Hierarchien der Konzerne. Spätestens dann verliert die Marktwirtschaft ihre innovative Kraft und gesamtgesellschaftliche Probleme (z.B. ökologische) bleiben in der Planung zugunsten der Egoismen der Hierarchien auf der Strecke.

Mein persönlicher Schluss: das Problem beweist tatsächlich, dass so etwas wie eine vollständige Planwirtschaft (wie jede genügend große Hierarchie!) nicht funktionieren kann. So weit so gut. Das spricht aber nicht gegen jede Form von wirtschaftlicher Planung, sondern heißt meines Erachtens, dass man sich in der Planung auf einige wesentliche (auf die planbaren) Grundsätze beschränken muss. Im Detail kann, soll und muss man mit dem Konkurrenzprinzip arbeiten; ihm ist die Tendenz zur Verbesserung, zur Innovation inhärent. Es geht allerdings darum, sicherzustellen, dass sich keine Monopole bilden, dass also die Innovationsvorteile erhalten bleiben.

Es entsteht damit ein „gemischtes“ Wirtschaftsmodell: der Rahmen wird geplant; innerhalb des Rahmens gilt das Prinzip der Konkurrenz, die Freiheit des Wirtschaftens; zum Rahmen gehören Gesetze, die (z.B.) die Bildung von Monopolen verhindern, die die sparsame Verwendung von Ressourcen regeln, die Menschen gegen die Verelendung schützen usw. usf. Man spricht z.B. von „(öko-)sozialer Marktwirtschaft“.

Historisch ist das „der dritte Weg“ zwischen marxistischer Planwirtschaft einerseits und liberaler Marktwirtschaft andrerseits. Historisch ist das die Position der Sozialdemokratie zwischen Kommunismus und Kapitalismus. Innerhalb der Renaissance des Kapitalismus als Neoliberalismus haben die Sozialdemokratien diese Position aber weitestgehend verlassen.

Es wäre extrem wichtig, sie wieder zu beleben.

… auch ein in seinen Grundzügen mindestens 10 Jahre alter Artikel, der nun endlich eine Form gefunden hat.